Add your promotional text...
My main research interests
Linear and nonlinear differential equations and their applications in Biology, Ecology, etc.
(Computational) Fluid Dynamics
Dynamical systems
My current research topic
My Ph.D. research project is Analysis and simulations of free boundary problems arising in biofilm modelling.
Background
Biofilms play a crucial role in the remediation of metal-laden wastewaters. Indeed, sorption of trace and contaminant metals on biofilm components represents to date one of the most promising, effective, and practical approaches for the bioremediation of metals and radionuclides, because of its efficiency, operation simplicity and availability of biomass. However, despite the continuing increases in published research, there has been little or no exploitation in the industrial context. This is probably related to the lack of knowledge on the multiplicity of mechanisms regulating the biosorption process (i.e., ion exchange, adsorption, micro-precipitation, and electrostatic and hydrophobic interactions). The global objective of my project is to a new modelling approach taking into account the various mechanisms regulating the TMs fate within biofilm systems: definition of differential equations governing the adsorption of trace metals on different fractions of the biofilm, such as extracelular polymers, cell membranes and cell walls, dead cells, or inert material, the biofilm dynamics in terms of microbial species growth and substrate consumption/production and transport.
The research
In this project, I am doing the following:
1) The review of literature: It's important to review the existing literature to fully grasp the existing gasps therein. For this part of my thesis, I and my supervisors preferred to look also at the numerical methods used to solve biofilms models. The idea is to kill two birds with one stone: we gain information on the advancement on biofilm modeling in general and we also study how numerical methods are often chosen to solve the biofilm model. Since the biofilm models are of several types, we focused on the continuous deterministic models comprising the most spread ones: the Wanner-Gurjer model, the Eberl model, the phase-field theory, and the mixture theory-inspired models. For each of this models the numerical methods propose vary greatly following the purpose of the study and the capability of the authors. A review paper on this work has been submitted.
2) Modeling precipitation: in this work, I propose a mathematical model that takes into account precipitates formation and their impact on the biofilm porosity (liquid phase). Indeed, the biofilm has 2 components: the solid and the liquid (porosity) phases. When precipitates form, they "clog" some "pores" of the biofilm (they occupy a part of the liquid phase). The model proposed is composed of a system of hyperbolic PDEs for the biofilm and the precipitates transport, a system of reaction-diffusion PDEs for the diffusion of nutrients in the biofilm, and an ODE for the thickness of the biofilm. The growth velocity equation is deduced from the biomass equation following the incompressibility constraint. The full model is a free boundary problem deduced from the well-konwn Wanner-Gurjer model. All the equations are derived following fluid dynamics laws, namely the conservation of mass. We will soon submit this work to a journal.These systems above all completed with appropriate boundary and initial conditions.
3) Qualitative analysis: Since its release in 1986, the Wanner-Gurjer model has never been completely studied qualitatively. Some partial studies exist but no study for both the global existence, the stationary solutions and the stability analysis was performed so far. I am doing a complete qualitative analysis of this model. This will lead to two different papers: one for the global existence and another for the stability analysis.
Scientific events
Oral presentation at the Internatonal conference on Mathematical Methods and Models and School of Young Scientists (BIOMATH2023) from 18 to 23 June 2023 in Pomorie, Bulgaria.
Oral presentation at the International congress on metal-micron applications for circular economy, IMAB23 Porto; University of Porto, Portugal, April 2023.
Oral presentation at the “Journées doctorales IMPEO”, University of Limoges, France, October 2022;
Workshop on biofilms and mini-symposium in Naples Organized by the University of Naples ‘’Federico II’’ from 4 to 8 July 2022.
A workshop on Science and society (Writing; presenting; communicating masterclass) and an M2ex Mini-symposium organized by the National University of Ireland, Galway from 18 to 22 April 2022.(Originally scheduled in Galway, it has been organized in Naples by the National University of Ireland, Galway from 11 to 12 July 2022);
A research school and workshop on Mathematical modelling of self-organization in medicine, biology, and ecology (MMSEOR2022), University of Palermo, Sicily, Italy, July 2022;
Hausdorff school on ‘Diffusive systems, Part II’ from 4 to 8 April 2022;
Workshop on nonlinear Partial differential equations, organized by the University of Salerno, Salerno, Italy;
Online Seminar on Numerics and Applications (SNAP) 1. organised by the group of research in Numerical analysis of the department of Mathematics and applications “Renato Caccioppoli” of the University of Naples “Federico”, Naples, Italy from May to October 2021 (one seminar each week);
Online Summer school on the qualitative theory of piecewise ordinary differential equations organized by the Centre de Recerca in Mathemàtica of the University of Barcelona, Catalonia, Spain from 12 to 16 July 2021;
Online Hausdorff Centre of Mathematics Seminar on diffusive systems: Pattern formation, bifurcations, and biological applications from 12 to 15 April 2021.
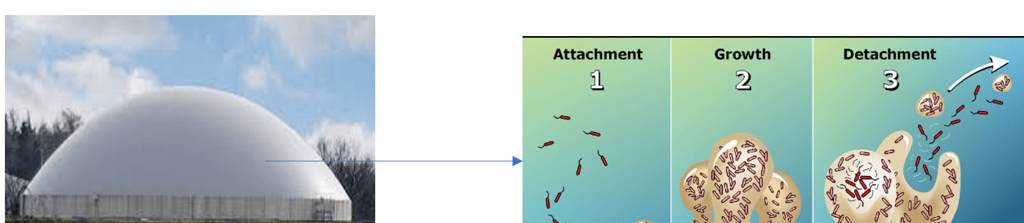
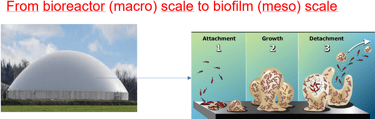
From Bioreactor to biofilm. What happens in bioreactor? When organic matters are introduced in wastewater treatment bioreactor, they are degradated by microorganisms called biofilms. These biofilms are communities of bacteria whose life can be described as follows: a normal lifecyle of a biofilm starts by attachment of small number of bacteria (phase 1), then they grow (phase 2), and they disperse (phase 3) because of washout or starvation.
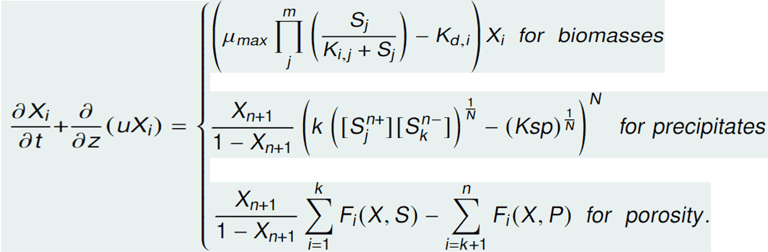
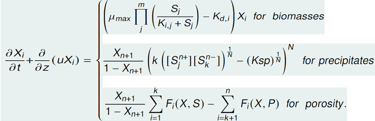
In summary, the biofilm model is made of:
1) A system of hyperbolic PDEs modeling the growth of the biomass, the transport of the precipitation, and the change in the liquid phase of the biofilm (biofilm porosity).
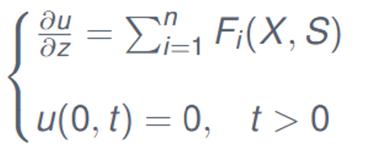
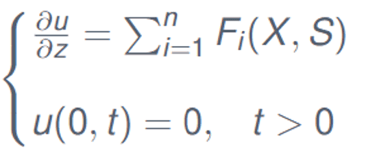
2) The velocity equation is derived from the incompressibility condition: all the biomass volume fractions sum up to 1.
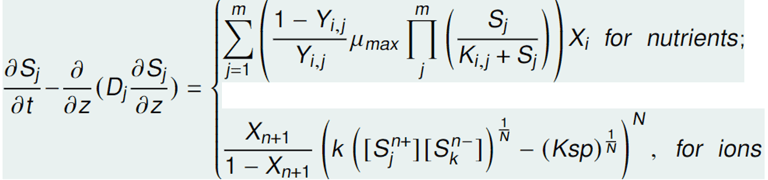
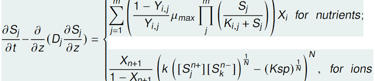
3) A system of parabolic PDEs for the substrates (nutrients) ions (anions and cations) diffusion in the biofilm.
4) The biofilm thickness and which stands for the free boundary of the problem.
Zirhumanana Balike Dieudonné
DZ Balike, L. Frunzo, MR Mattei, F. Russo, Existence and uniqueness of solution to a hyperbolic-parabolic free boundary problem for biofilm growth https://arxiv.org/abs/2411.17974
DZ Balike, L. Frunzo, V. Deuchat, V. Luongo, MR. Mattei, Mathematical modeling of trace-metals precipitation in biofilms https://biomath.math.bas.bg/biomath/index.php/bmcs/article/view/1583
DZ Balike, L. Frunzo, MR. Mattei, Stability analysis of hyperbolic-parabolic free boundary problems modelling biofilms, https://arxiv.org/abs/2411.16977
Z. Balike, Mathematical model for the mitigation of the economic effects of the Covid-19 in the Democratic Republic of the Congo, PLOS ONE, 2021
Z. Balike, A. Ring, M. Saiguran, Modeling the movements of particles in tilings by Markov chains, Open Journal of Mathematical Analysis, 2020